https://www.acmicpc.net/problem/2118
문제
1번부터 N번까지의 지점이 있다. 각각의 지점들은 차례로, 그리고 원형으로 연결되어 있다. 이 지점들 중 두 곳에 두 개의 탑을 세우려고 하는데, 두 탑의 거리가 최대가 되도록 만들려고 한다.
지점들이 원형으로 연결되어 있기 때문에, 두 지점 사이에는 시계방향과 반시계방향의 두 경로가 존재한다. 두 지점 사이의 거리를 잴 때에는, 이러한 값들 중에서 더 작은 값을 거리로 한다.
연결되어 있는 두 지점 사이의 거리가 주어졌을 때, 두 탑의 거리의 최댓값을 계산하는 프로그램을 작성하시오.
입력
첫째 줄에 지점의 개수 N(2 ≤ N ≤ 50,000)이 주어진다. 다음 N개의 줄에는 차례로 두 지점 사이의 거리가 양의 정수로 주어진다. 전체 거리의 총 합은 1,000,000,000을 넘지 않는다.
출력
첫째 줄에 답을 출력한다.
문제 풀이
투 포인터를 이용한 문제.
탑끼리의 거리 중 두 부분으로 나누었을 때 작은 값을 찾는다. '두 부분으로 나누었을 때 작은 값'을 투 포인터를 이용해 해결할 것이다. 한 포인트(start)를 고정해놓고, 다른 한 포인트(end)까지의 거리가 최대가 되면서 전체 탑끼리의 거리 중 1/2을 넘지 않아야 한다. 탑은 원형으로 구성되어있으므로 투포인터에서 입력한 값의 뒷부분이 앞부분의 값을 접근할 수 있게 하기 위해 배열의 크기는 2*N으로 잡아 N부터 2N - 1까지는 중복으로 값을 저장한다.
end를 증가시키며 현재 start에서 얻을 수 있는 최대 거리를 구하고, start를 증가시켜가며 반복적으로 최대 거리를 구해주면 된다.
예제 입력 1 2 3 4 5로 예시를 들어보자.
전체 총 합은 15이므로, start-end를 정하는 한 회차의 탐색에서 얻을 수 있는 최대 값은 7이 될 것이다.
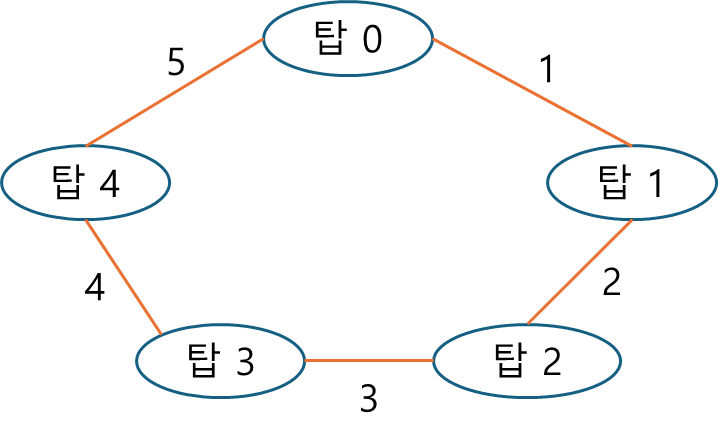
start가 0일 때, end는 3까지 이동하여 최대 거리는 6이다. 이는 탑 0을 첫 지점으로 선택했을 때 탑 3을 선택하면 최대 거리를 얻을 수 있고, 이 때의 거리는 6이라는 뜻이다.
start가 1일 때 end는 3이며, 최대 거리는 5이다. 이는 탑 1을 첫 지점으로 선택한다면 탑 3을 선택하면 최대 거리가 되고, 이 때의 거리는 5라는 뜻이다.
start가 2일 때 end는 4이며, 이 때의 거리는 7이다. 탑 2를 첫 지점으로 선택하면 탑 4를 선택했을 때 거리 7의 최대가 된다.
start가 3일 때 end는 4이며, 이 때의 거리는 4가 된다. 탑 3을 첫 지점으로 선택한다면 탑 4를 선택했을 때 거리 4의 최대가 된다.
start가 4일 때 end는 6이며, 이 때의 거리는 6이 된다. 탑 4를 첫 지점으로 선택한다면 탑 1을 선택했을 때 거리 6의 최대가 된다.
따라서 정답은 7이 된다.
아래는 코드.
#include <iostream>
using namespace std;
int main()
{
cin.tie(NULL);
ios::sync_with_stdio(false);
int N;
cin >> N;
int* arr = new int[2 * N];
int distanceSum = 0;
int currentDistance = 0;
int answer = 0;
int start = 0;
int end = 0;
for (int i = 0; i < N; i++)
{
cin >> arr[i];
distanceSum += arr[i];
}
for (int i = N; i < 2 * N; i++)
{
arr[i] = arr[i - N];
}
while (start < N)
{
while (true)
{
currentDistance += arr[end];
if (currentDistance > distanceSum / 2)
{
currentDistance -= arr[end];
break;
}
end++;
}
if (currentDistance > answer)
{
answer = currentDistance;
}
currentDistance -= arr[start];
start++;
}
cout << answer << "\n";
return 0;
}'알고리즘 > 백준' 카테고리의 다른 글
| [백준 11899] 괄호 끼워넣기 (C++) (0) | 2024.05.04 |
|---|---|
| [백준 2659] 십자카드 문제 (C++) (0) | 2024.05.03 |
| [백준 8901] 화학 제품 (C++) (0) | 2024.05.01 |
| [백준 6198] 옥상 정원 꾸미기 (C++) (0) | 2024.04.30 |
| [백준 2591] 숫자카드 (C++) (0) | 2024.04.29 |
