https://www.acmicpc.net/problem/11909
11909번: 배열 탈출
상수는 2차원 배열 A[1..n][1..n] (n≥2, n은 자연수)을 가지고 있습니다. 이 배열의 각 원소는 1 이상 222 이하의 정수입니다. 배열을 가지고 놀던 상수를 본 승현이는, 질투심이 불타올라 상수를 A[1][1]
www.acmicpc.net
문제
상수는 2차원 배열 A[1..n][1..n] (n≥2, n은 자연수)을 가지고 있습니다. 이 배열의 각 원소는 1 이상 222 이하의 정수입니다.
배열을 가지고 놀던 상수를 본 승현이는, 질투심이 불타올라 상수를 A[1][1]에 가둬 버렸습니다! 최소한의 양심이 있던 승현이는 A[n][n]에 출구를 만들어 놓고 이 사실을 상수에게 알려줬습니다.

[그림 1] n=4라면 상수는 A[1,1]에 있고, 출구는 A[4][4]에 있습니다.
상수는 가능한 한 빨리 출구인 A[n][n]에 도달하고자 합니다. 상수가 A[i][j]에 있다고 가정했을 때, 상수는 최단 경로로 이동하기 위해 아래와 같은 조건을 만족하며 이동합니다.
- 1≤i,j<n이라면, 상수는 A[i][j+1] 또는 A[i+1][j]로만 건너갑니다.
- i=n,1≤j<n이라면, A[i][j+1]로만 건너갑니다.
- 1≤i<n,j=n이라면 A[i+1][j]로만 건너갑니다.
- i=j=n인 경우 바로 출구로 갑니다.

[그림 2] n=5라고 가정합시다. (ㄱ)는 1번 조건을 만족하고, (ㄴ)는 2번 조건을 만족하며, (ㄷ)는 3번 조건을 만족합니다.
그러나 건너갈 때에도 제약이 따릅니다. 상수가 A[a][b]에서 A[c][d]로 건너가려면 A[a][b]>A[c][d]를 만족해야 합니다. 상수는 왜인지 이런 조건을 만족하면서 이동할 수 없을 것 같았습니다. 다행히도, 승현이가 상수를 배열에 가둬버리기 전에, 상수는 배열의 각 원소에 버튼을 만들어 놓아서, 이 버튼을 누르면 해당 원소의 값이 1 증가하도록 했습니다. (물론 상수는 자신이 위치해 있는 원소의 버튼만 누를 수 있습니다.) 이 버튼 덕분에, 상수는 항상 배열을 탈출할 수 있습니다!
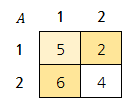
[그림 3] n=2라고 가정합시다. A[1][1]=5>A[1][2]=2이므로, 상수는 A[1][1]에서 A[1][2]로 건너갈 수 있습니다.
상수가 A[1][1]에서 A[2][1]로 건너가려면, A[1][1]에 있는 버튼을 두 번 눌러 A[1][1]의 값을 7로 만들면 됩니다.
하지만 버튼을 한 번 누르는 데에는 1원의 비용이 듭니다. 상수는 돈을 가능한 한 적게 들이면서 배열을 탈출하고자 합니다. 상수를 도와주세요.
입력
첫 번째 줄에 n이 주어집니다. (n ≤ 2,222)
다음에 n개 줄이 주어집니다. 이 중 i(1≤i≤n)번째 줄에는 n개의 수 A[i][1],A[i][2],⋯,A[i][n−1],A[i][n]이 공백을 사이로 두고 차례대로 주어집니다.
출력
첫 번째 줄에 상수가 배열을 탈출하기 위해 들여야 할 최소 비용(원 단위)을 출력합니다.
문제 풀이
dp 문제.
A[i][j]는 A[i][j-1]과 A[i-1][j]에서 오는 두 가지 경우가 있다. 따라서 A[i][j-1]과 A[i-1][j]까지의 최소 비용을 각각 구한 후 그 값에 A[i][j]로 오기 위해 추가로 지불해야 하는 비용을 더한다. 두 값 중 작은 값이 A[i][j]까지 가는데 필요한 최소 비용이다.
아래는 코드.
#include <iostream>
using namespace std;
int main()
{
cin.tie(NULL);
ios::sync_with_stdio(false);
int N;
cin >> N;
int** arr = new int* [N];
int** dp = new int* [N];
for (int i = 0; i < N; i++)
{
arr[i] = new int[N];
dp[i] = new int[N];
for (int j = 0; j < N; j++)
{
cin >> arr[i][j];
dp[i][j] = 987654321;
}
}
dp[0][0] = 0;
for (int i = 1; i < N; i++)
{
if (arr[0][i] >= arr[0][i - 1])
{
dp[0][i] = dp[0][i - 1] + arr[0][i] - arr[0][i - 1] + 1;
}
else
{
dp[0][i] = dp[0][i - 1];
}
}
for (int i = 1; i < N; i++)
{
if (arr[i][0] >= arr[i - 1][0])
{
dp[i][0] = dp[i - 1][0] + arr[i][0] - arr[i - 1][0] + 1;
}
else
{
dp[i][0] = dp[i - 1][0];
}
}
for (int i = 1; i < N; i++)
{
for (int j = 1; j < N; j++)
{
int down, right;
if (arr[i][j - 1] <= arr[i][j])
{
right = arr[i][j] - arr[i][j - 1] + 1;
}
else
{
right = 0;
}
if (arr[i - 1][j] <= arr[i][j])
{
down = arr[i][j] - arr[i - 1][j] + 1;
}
else
{
down = 0;
}
dp[i][j] = min(dp[i-1][j] + down, dp[i][j-1] + right);
}
}
cout << dp[N-1][N-1] << "\n";
return 0;
}'알고리즘 > 백준' 카테고리의 다른 글
| [백준 14658] 하늘에서 별똥별이 빗발친다 (C++) (0) | 2024.02.25 |
|---|---|
| [백준 12789] 도키도키 간식드리미 (C++) (0) | 2024.02.23 |
| [백준 22115] 창영이와 커피 (C++) (0) | 2024.02.21 |
| [백준 2143] 두 배열의 합 (C++) (0) | 2024.02.20 |
| [백준 26123] 외계 침략자 윤이 (C++) (0) | 2024.02.18 |
