https://www.acmicpc.net/problem/1915
1915번: 가장 큰 정사각형
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
www.acmicpc.net
문제
n×m의 0, 1로 된 배열이 있다. 이 배열에서 1로 된 가장 큰 정사각형의 크기를 구하는 프로그램을 작성하시오.
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 |
위와 같은 예제에서는 가운데의 2×2 배열이 가장 큰 정사각형이다.
입력
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
출력
첫째 줄에 가장 큰 정사각형의 넓이를 출력한다.
문제 풀이
길이 n짜리 정사각형을 만드려면 n-1짜리 정사각형의 오른쪽 1열이 길이 n - 1만큼 있어야 하며, 아래쪽 1행이 길이 n - 1만큼 있어야 한다. 또한 n-1짜리 정사각형의 우하단 좌표를 [i-1][j-1]라고 한다면 [i][j] 역시 1이어야 한다.
[i][j]의 관점에서 보면 위쪽은 n-1개 연속으로 1이 있어야 하며, 왼쪽은 n-1개 연속으로 1이 있어야 하며, [i-1][j-1]는 n-1*n-1 크기의 정사각형의 우하단이어야 한다.
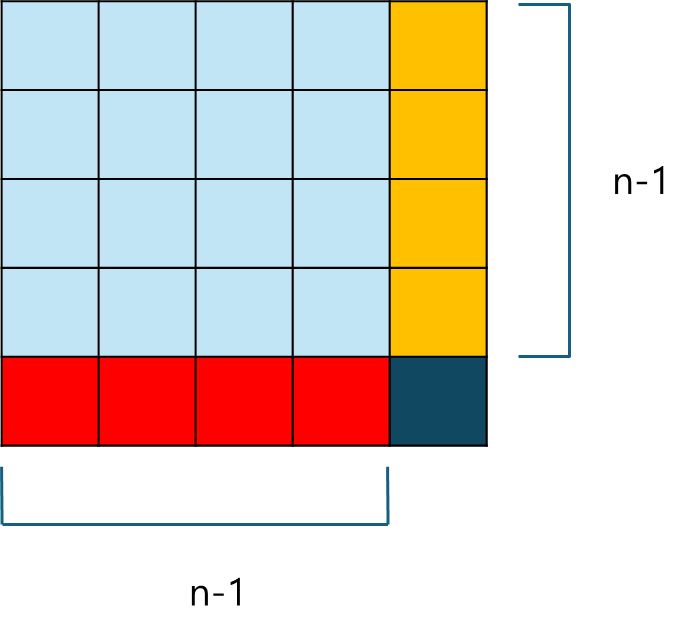
만약 다음과 같이 위쪽 연속으로 1이 나오는 길이와 왼쪽 연속으로 1이 나오는 길이가 다르다면 짧은 쪽 길이에 1을 더한 값이 만들 수 있는 정사각형의 가장 긴 길이가 된다.

만약 다음과 같이 [i-1][j-1]에서 만들어질 수 있는 정사각형 변의 길이가 위쪽과 왼쪽에서 얻어질 수 있는 길이보다 작다면 [i-1][j-1]에 맞춰져 [i][j]에서 만들 수 있는 가장 큰 정사각형의 길이는 [i-1][j-1]에서 만들 수 있는 가장 긴 길이+1이 된다.

본인을 포함하여 왼쪽에 1이 몇개 존재하는지 저장하는 left, 위쪽에 1이 몇 개 존재하는지 저장하는 right, 해당 위치를 우하단으로 삼는 가장 큰 정사각형의 길이를 저장하는 maxLength 배열을 만들어 위의 조건에 맞게 배열을 채운다.
그 후 maxLength배열 전체를 탐색하며 가장 큰 정사각형의 넓이를 찾는다.
아래는 코드.
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
cin.tie(NULL);
ios::sync_with_stdio(false);
int N, M;
string str;
cin >> N >> M;
int** arr = new int*[N];
int** left = new int* [N];
int** up = new int* [N];
int** maxLength = new int*[N];
int answer = 0;
for (int i = 0; i < N; i++)
{
arr[i] = new int[M];
left[i] = new int[M];
up[i] = new int[M];
maxLength[i] = new int[M];
cin >> str;
for (int j = 0; j < M; j++)
{
arr[i][j] = str.at(j) - 48;
left[i][j] = 0;
up[i][j] = 0;
maxLength[i][j] = 0;
}
}
if (arr[0][0] == 1)
{
maxLength[0][0] = 1;
left[0][0] = 1;
up[0][0] = 1;
}
for (int i = 1; i < M; i++)
{
if (arr[0][i] == 1)
{
left[0][i] = left[0][i - 1] + 1;
up[0][i] = 1;
maxLength[0][i] = 1;
}
}
for (int i = 1; i < N; i++)
{
if (arr[i][0] == 1)
{
up[i][0] = up[i - 1][0] + 1;
left[i][0] = 1;
maxLength[i][0] = 1;
}
}
for (int i = 1; i < N; i++)
{
for (int j = 1; j < M; j++)
{
if (arr[i][j] == 1)
{
int fromLeft = left[i][j-1];
int fromUp = up[i - 1][j];
left[i][j] = fromLeft + 1;
up[i][j] = fromUp + 1;
int length = min(fromLeft, fromUp);
if (length >= 1)
{
if (maxLength[i - 1][j - 1] < length)
{
maxLength[i][j] = maxLength[i - 1][j - 1] + 1;
}
else
{
maxLength[i][j] = length + 1;
}
}
else
{
maxLength[i][j] = 1;
}
}
}
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
answer = max(answer, maxLength[i][j] * maxLength[i][j]);
}
}
cout << answer << "\n";
return 0;
}'알고리즘 > 백준' 카테고리의 다른 글
| [백준 30022] 행사 준비 (C++) (0) | 2024.03.05 |
|---|---|
| [백준 25045] 비즈마켓 (C++) (0) | 2024.03.03 |
| [백준 11688] 최소공배수 찾기 (C++) (0) | 2024.02.29 |
| [백준 1509] 팰린드롬 분할 (C++) (0) | 2024.02.28 |
| [백준 15990] 1, 2, 3 더하기 5 (C++) (0) | 2024.02.27 |
